[알고리즘] Chapter 3

알고리즘 효율성 분석

알고리즘의 효율성 분석은 반복문을 얼마나 사용했는지에 따라 효율성이 결정된다. 또한, 특정 한줄을 실행할 때 operation이 얼마나 실행이 됐는지를 따져서 효율성을 결정한다.

알고리즘 효율성 분석에는 아래와 같은 요소가 있다.

• 효율성(Efficiency) : 시간과 공간의 효율성

• 간소성(Simplicity) : 이해와 구현하기가 쉬운가

• 범용성(Generality) : 문제의 범용성과 입력의 범위

• 최적성(Optimality) : 다른 알고리즘이 더 잘할 수 있는가

실행 시간 분석하기

그래서 시간을 어떻게 분석할 것인가? 시간은 컴퓨터의 속도에 따라, 알고리즘의 설계에 따라, 입력 데이터에 따라 나뉠 것이다.

여러 요소가 있기에, 컴퓨터의 속도는 무한정 빠르다고 가정하자.

무한한 입력 데이터에 따른 알고리즘 설계로 인한 시간은 어떻게 결정될까? 이는 함수의 성장성에 기반하고, 이를 정확히 아는 것은 불가능하기에 점근표기법을 사용하게 된다.

성장성

n 이 커짐에 따라, 정의된 시간 효율성에서 각각의 항(term)이 영향력을 행사하는 정도가 다르다.

예를들어, n은 n^2 보다 n 값이 커짐에 따라 끼치는 영향력이 n의 제곱보다 훨씬 작을 것이다.

성장성을 고려한 각각의 효율성 분류는 1부터 팩토리얼까지 다양하다.

• 1 : (상수)
• log n
• n log n : 여기까지 실용적이다.
• n
• n^2
• n^3 : 여기까지는 다항시간이다.
• 2^n : 여기서부터는 너무 커서 의미가 없다. (NP문제)
• n!

시간 효율성에 따른 수식의 유형

아래 함수들은 시간 효율성에 따른 실행시간을 표기한 여러 함수 표현들이다.

• F(n) : n의 크기에 따른 일반적인 실행 시간의 수식 ex. 1.5x^2 + sin(12x) + 128

• g(n) : 성장성 을 고려한 F(n) 함수 ex. x^2

• T(n) : 각각의 case 에 따른 입력크기 n 에 따른 수행시간.

점근 표기법

무한히 크는 N에 대해 알고리즘의 시간복잡도를 정확히 표현하기가 어려워서 각각의 경우의 수에 대한 시간 복잡도 표현을 아래와 같이 표현한다.

• Big - O Notation (worst case): N이 커질 수록, 이 함수보단 빠를 것이다. 라는 뜻이다.

• Big - Omega Notation (best case) : N이 커질 수록 아무리 빨라도 이 함수보단 느리다는 뜻이다. (최선이 이만큼)

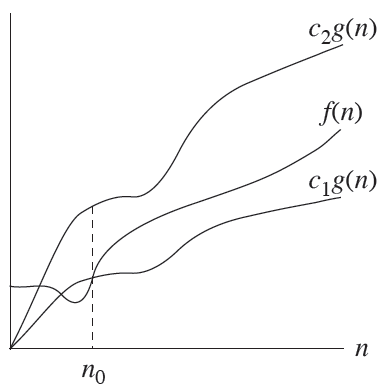
• Big theta Notation : N이 커질 수록 특정 두 함수 클래스 사이에 함수 f(n)이 존재할 것이다

대부분 계산하기도 쉽고, 상정하기도 쉬운 worst case(이 함수보단 빠르다 라는 것을 암시한다.) Big - O Notation 을 많이 사용한다.

따라서 위에서 언급한 F(N) 은 점근 표기법에서는 성장성을 고려한 함수 g(N) 을 이용하여 표기하면, O(g(N)) … 이 되는 것이다.

예시 : 정렬 문제에 대한 효율성 분석

저번 시간에 언급한 삽입 정렬 에 대해 분석을 해보자. 아래는 저번 강의에서 언급한 삽입정렬의 의사코드이다.

A[] 는 입력된 배열

for j <- 2 to N
    do key <- A[j]
        i <- j-1 // i는 j-1부터 1까지 순회를 할 것이다.
        while i > 0 and A[i] > key
            do A[i + 1] <- A[i]
                i <- i-1
        A[i+1] <- key

각각의 한줄은 연산을 실행하며, 비교연산 또한 하나의 연산으로 취급하므로 for 문에서는 n-1번 반복한다해도 종료조건을 계산하기 때문에 +1 을 해야한다.

T(n) 계산하기

위 의사코드로부터 각각의 한 줄은 계산하는 시간은 모두 다르게 책정해야한다.

예를들어, 첫줄의 for 문은 c1 만큼의 시간이 걸리고, 그 다음줄의 연산은 c2만큼 걸린다고 가정하자.

A[] 는 입력된 배열

for j <- 2 to N                                      | c1
    do key <- A[j]                                   | c2
    i <- j-1 // i는 j-1부터 1까지 순회를 할 것이다.         | c3
    while i > 0 and A[i] > key                       | c4
        do A[i + 1] <- A[i]                          | c5
            i <- i-1                                 | c6
    A[i+1] <- key                                    | c7

또한, 반복문에서 예를들어 for 문을 i가 1부터 N까지 돌아간다고 칠 때, 위에서 언급했듯 종료 조건을 연산해야하기 때문에 for 문에서 i를 비교하는 과정은 N + 1 번 수행되게 된다. 이를 감안하여 계산을 하자.

while의 경우 입력에 따라 결과가 달라질 수도 있으므로 아예 while 루프가 얼마나 도는지 횟수를 j에 대해 정의를 하였으니, t_j 와 같이, 별도의 값으로 정의하여 문제를 해결하기도 한다. (j 번째 항에 따라 걸리는 정도를 일반화하여 t_j라고 표현)

그럼, 앞서 언급한 것들을 감안하여 각각의 항이 몇번씩 연산되는지를 고려하여, 반복되는 횟수만큼 곱해주면 아래 코드와 같아진다.

A[] 는 입력된 배열

for j <- 2 to N                                      | c1 * (n)
    do key <- A[j]                                   | c2 * (n-1)
    i <- j-1 // i는 j-1부터 1까지 순회를 할 것이다.         | c3 * (n-1)
    while i > 0 and A[i] > key                       | c4 * (Sigma 2 to N - t_j)
        do A[i + 1] <- A[i]                          | c5 * (Sigma 2 to N - t_j - 1)
            i <- i-1                                 | c6 * (Sigma 2 to N - t_j - 1)
    A[i+1] <- key                                    | c7 * (n-1)

이를 바탕으로 T(n)은 아래와 같은 공식으로 수식화할 수 있다.

T(n) = c1n + c2(n-1) + c3(n-1) + c4(Sigma(2 to N)[t_j]) + c5(Sigma(2 to N)[t_j - 1])
    + c6(Sigma(2 to N)[t_j - 1]) + c7(n-1)

Best Case 에 대해 계산하기

여기서 가변적으로 변할 수 있는 N에 대한 공식은 t_j 일 것이다.

t_j 를 최소화 할 수 있는 경우의 수가 무엇일까? 바로 A[i = j-1] <= key(A[j]) 인 경우의 수 일 것이다. 이렇게 된다면 t_j는 모든 경우에 대해 1이 될 것이기 때문

그런데, 이러한 경우는 이미 정렬된 경우 밖에 없다. 따라서 해당 케이스에 대한 T(n) 은 아래와 같이 된다.

T(n) = c1n + c2(n-1) + c3(n-1) + c4(n-1) + c7(n-1)

Worst Case 에 대해 계산하기

반대로 worst case는 i가 1일때까지 A[i] > key 를 모든 경우에도 만족하는 입력이 될 것이다.

그런데, 이러한 경우의 수는 사실 반대로 생각하면 최선의 경우의 수 처럼 역순으로 정렬이 되어있는 경우밖에 없다.

따라서 이때의 입력은 역순으로 정렬된 배열일 것이고, t_j = j 이다. 왜 j 냐면 j 번 반복하기 때문이다.

T(n) = c1n + c2(n-1) + c3(n-1) + c4(Sigma(2 to N)[t_j]) + c5(Sigma(2 to N)[t_j - 1])
    + c6(Sigma(2 to N)[t_j - 1]) + c7(n-1)
    
     = c1n + c2(n-1) + c3(n-1) + c4(n(n+1)/2 - 1) + c5(n(n-1)/2) + c6(n(n-1)/2) + c7(n-1)

F(n) 계산하기

F(n) 의 경우 우리는 점근 표기법으로 접근하게 된다.

F(n)이 우리가 아는 간소화된 g(n)의 공식을 이용해 최소 / 최대 / 사이에 적어도 반드시 있을 것이라 추측하는 방식으로 접근하여 유추를 하는 방향이 일반적인 것 같다.

T(n)에서 가장 성장성이 강한 term 이 무엇인가?

이는 각각의 경우의 수에 대해 생각을 해봐야할 것이다.

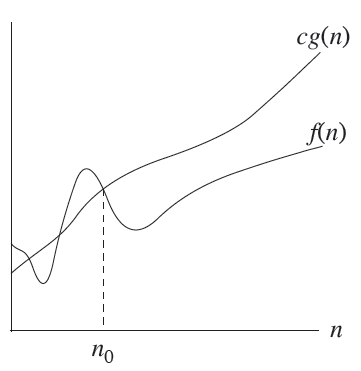
Big - O Notation으로 표현하기

점근적 상한이라고 생각하면 편하겠다. 점근적으로 보면 궤를 같이하나, 미지의 f(n) 보다는 큰 g(n) 이 존재한다는 뜻이다.

여기서는 가장 느린 Worst Case 가 어떤 n^2 클래스에 속하는 g(n) 보다는 느릴 것이라고 추론할 수 있다.

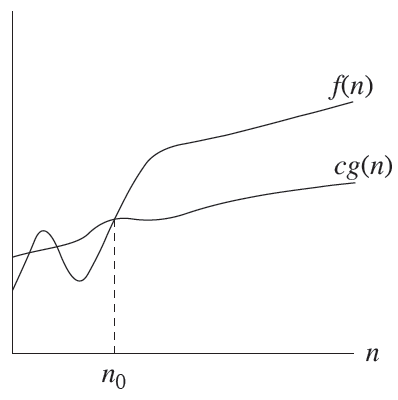
Big - Omega Notation 으로 표현하기

마찬가지로 점근적 하한이라고 생각하면 된다. 점근적으로 보면 궤를 같이 하나, 미지의 f(n)보다는 작은 g(n)이 존재한다.

이제 여기에서는 가장 빠른 Best Case가 g(n) = n 보다는 빠르지만, 같은 클래스에 속하는 함수 이므로,

오메가 노테이션으로 삽입정렬은 _O_(n) 이라고 생각하면 되겠다.

Big - Theta Notation 으로 표현하기